Triplet lacing (AKA 2:1 lacing)
| Left | Right | |
| Spoke length | ||
| Tension distribution NOTE: left tension will be roughly twice what this currently computes! |
||
| Spoke head clearance NOTE: left side math needs to be verified! |
||
| Bracing angle | ||
| Wrap angle (at rim) | ||
| Total angle at rim | ||
| Effective tangential PCD | ||
| Flange exit angle | ||
| Theta angle |
This is a lacing pattern where there are two right spokes for every left spoke. The stated goal is to increase tension on the left side spokes (by having half as many as usual). What this actually does to wheel strength and durability is left as an exercise for the user. It is possible to use "normal" rims and hubs (drilled in multiples of 4) to achieve this lacing, but only with a few speific combinations that fit the 2:1 criteria.
Requirements:
- A standard drilling is divisible by 4, and is equally spaced around the hub/rim. 48, 40, 36, 32, 28, 24, 20, etc.
- The rim must have 3/4 the number of holes as the hub. The only two possible combinations that use standard parts are 48h hub to 36h rim and 32h hub to 24h rim. Possible combinations using nonstandard-drilled rims but standard hubs include 40h hub to 30h rim, 36h hub to 27h rim, 28h hub to 21h rim, 24h hub to 18h rim, and 20h hub to 15h rim.
- The rim must be drilled such that holes intended for left and right flanges can be used interchangeably (you will be lacing RRLRRLRRLRRL instead of RLRLRLRLRL at the rim)
- Stagger (left/right) of the rim holes/eyelets should be nonexistant or at least negligible (see above).
- The rim's holes must be spaced evenly. (paired or uneven spacing would require a more complex formula than this page currently uses; it's in the works eventually)
- The hub's holes must be spaced evenly on both flanges and the two flanges clocked one half hole apart (like any common hub).
- It would be wise to use a rim with a relatively stout cross section, since left side spokes are a long ways apart and there are always two right side spokes between them.
Hub Rim 48 36 44* 33* 40 30* 36 27* 32 24 28 21* 24 18* (*denotes nonstandard drilling)
Typically, the right side spokes are laced with a cross patternand the left side spokes are laced radially. There is nothing to stop you from crossing the left side spokes, and symmetrical patterns should easily result, but you'll need to be careful to select the correct left flange holes.
Unlike with a common lacing pattern, there are effectively positive and negative cross patterns. There seems to be no mathematically-based way of assigning positive or negative to each of these (as best as I can figure), so I have arbitrarily assigned them. Locate a pair of neighboring right side spokes on the rim (neighboring meaning there is not a left spoke between them) and follow them to the hub flange. If they cross one another, this is a negative cross pattern. If they do not cross one another, this is a positive cross pattern.
Manufacturers commonly associated with triplet-laced wheels are Campagnolo and Fulcrum, but Roval and even Shimano have dabbled in this realm.
For example, Campy triplet-laced rear wheels use what I am calling a negative cross pattern, while Fulcrum wheels use a positive cross pattern. To determine, find a pair of drive side spokes that are adjacent neighbors at the rim (even if there is a notable space between them). If they cross on the way to the hub, they are laced with a negative cross pattern, and if they do not cross they are laced with a positive cross pattern. To calculate for a negative three-cross lacing pattern, literally enter -3 for the right side cross pattern.
The author of this post about triplet lacing refers to these two patterns as "type 1" and "type 2". The ASCII art used to visually differentiate the two is not 100% foolproof, as both lacing patterns have drive side crossing in front of each radial spoke, just at different elevations off the hub.
A zero-cross drive side lacing will not be perfectly radial. The mismatch in drillings means there is not a hub flange hole directly between the axle and the rim hole. The correct clocking of rim and hub is with the left (non-drive) rim and hub holes aligned with the axle to allow the left spokes to be exactly radial. Between every two left spokes are two rim holes and three hub flange holes, so they cannot all lay on radial lines like on a conventional wheel.
Sheldon Brown's site has an excellent breakdown of how the basic spoke length formula works. Normally the theta value is determined with a simple formula taking into account drilling and cross pattern, but this assumes you are building a conventionally-laced wheel. Instead, we are going to be using the theta values shown above (derived in CAD, but a formula would not be very difficult). These theta values work for equally spaced rim and hub holes (conventional parts).
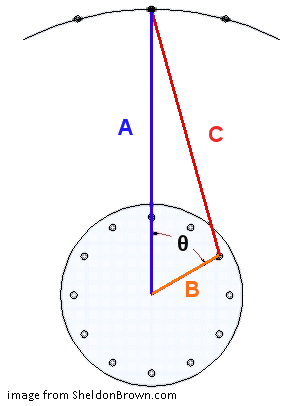
Wrap angle (theta) is the angle between a line from the axle to the rim hole and a second line from the axle to the hub hole. For a conventional lacing pattern, this can be calculated as 360 * [cross pattern] / ([number of spokes] / 2). Life gets a little harder when we mismatch the hole count of the rim and hub, because the hub flange holes no longer all lie on radial lines between the axle and rim holes. For this lacing system, all of the left spokes are on radial lines, and all of the right spokes must necessarily be slightly off a radial line even if laced zero cross.
hub wrap angles (theta) for 32/24 combo right side spokes: +4x 93.75° (bad idea; way more than tangential for any part combo) +3x 71.25° +2x 48.75° +1x 26.25° 0x 3.75° -1x -18.75° -2x -41.25° -3x -63.75° -4x -86.25° (probably almost exactly tangential depending on ERD and PCD. Watch spoke head clearance though!) each distinct type of 32/24 spokes repeat every 45 degrees (360 / 24 holes * 3rd rim hole) hub wrap angles (theta) for 48/36 combo right side spokes: +4x 62.5° +3x 47.5° +2x 32.5° +1x 17.5° 0x 2.5° -1x -12.5° -2x -27.5° -3x -42.5° -4x -57.5° each distinct type of 48/36 spokes repeat every 30 degrees (360 / 36 * 3rd rim hole)
The zero-cross angle is calculated as ((360/rim)-(360/hub)). Each cross more or less is adding or subtracting (cross*(360/(hub/2))) from this base value.
You might be wondering: Why is this referred to as 2:1 lacing when all of these ratios are actually 4:3? There are two drive side spokes for each one non-drive spoke (2:1) but only half of the left hub flange holes are populated. A 32h hub laced to a 24h rim with this method will use all 16 right flange holes, but only 8 left flange holes (and 8 are left empty). 16:8 = 2:1.